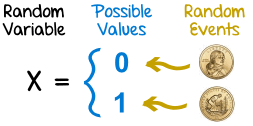What is the difference between Probability and Statistics?

Nice clear explanation of the difference. This should be given in every statistical/probability course.

In probability, we start with a model describing what events we think are going to occur, with what likelihoods. The events may be random, in the sense that we don’t know for sure what will happen next, but we do quantify our degree of surprise when various things happen.

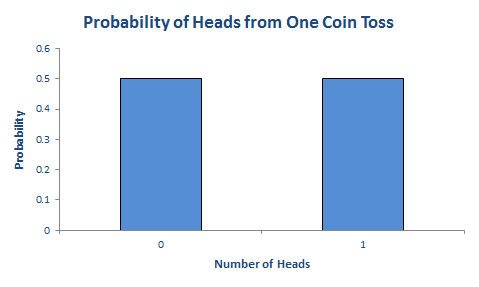
The standard (maybe overused) example is flipping a fair coin. “Fair” means, technically, that the probability of heads on a given flip is 50%, and the probability of tails on a given flip is 50%. This doesn’t mean that every other flip will give a head — after all, three heads in a row is no surprise. Five heads in a row would be more surprising, and when you’ve seen twenty heads in a row you’re sure that something fishy is going on. What the 50% probability of heads does mean is that, as the number of flips increases, we expect the number of heads to approach half the number of flips. Seven heads on ten flips is no surprise; 700,000 heads on 1,000,000 tosses is highly unlikely.

Another example would be flipping an unfair coin, where we know ahead of time that there’s a 60% chance of heads on each toss, and a 40% chance of tails.

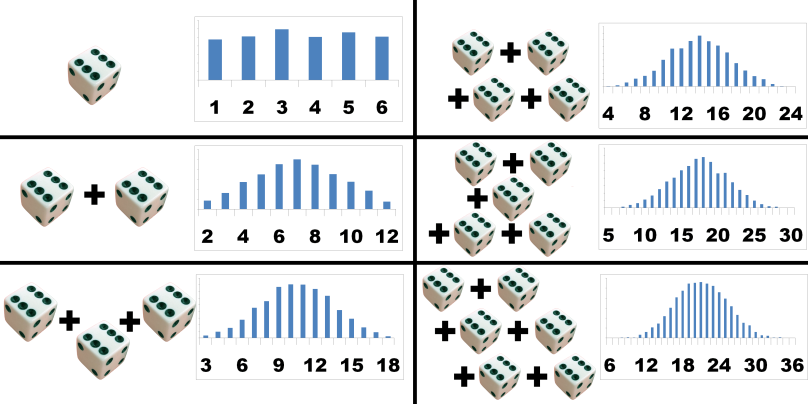
A third example would be rolling a loaded die, where (for example) the chances of rolling 1, 2, 3, 4, 5, or 6 are 25%, 5%, 20%, 20%, 20%, and 10%, respectively. Given this setup, you’d expect rolling three 1’s in a row to be much more likely than rolling three 2’s in a row.

As these examples illustrate, the probabilist starts with a probability model (something which assigns various percentage likelihoods of different things happening), then tells us which things are more and less likely to occur.

Key points about probability:

1. Rules → data: Given the rules, describe the likelihoods of various events occurring.
2. Probability is about prediction — looking forward.
3. Probability is mathematics.

---

The statistician turns this around:

1. Rules ← data: Given only the data, try to guess what the rules were. That is, some probability model controlled what data came out, and the best we can do is guess — or approximate — what that model was. We might guess wrong; we might refine our guess as we get more data.
2. Statistics is about looking backward.
3. Statistics is an art. It uses mathematical methods, but it is more than math.
4. Once we make our best statistical guess about what the probability model is (what the rules are), based on looking backward, we can then use that probability model to predict the future. (This is, in part, why I say that probability doesn’t need statistics, but statistics uses probability.)

Here’s my favorite example to illustrate. Suppose I give you a list of heads and tails. You, as the statistician, are in the following situation:

• You do not know ahead of time that the coin is fair. Maybe you’ve been hired to decide whether the coin is fair (or, more generally, whether a gambling house is committing fraud).
• You may not even know ahead of time whether the data come from a coin-flipping experiment at all.

Suppose the data are three heads. Your first guess might be that a fair coin is being flipped, and these data don’t contradict that hypothesis. Based on these data, you might hypothesize that the rules governing the experiment are that of a fair coin: your probability model for predicting the future is that heads and tails each occur with 50% likelihood.

If there are ten heads in a row, though, or twenty, then you might start to reject that hypothesis and replace it with the hypothesis that the coin has heads on both sides. Then you’d predict that the next toss will certainly be heads: your new probability model for predicting the future is that heads occur with 100% likelihood, and tails occur with 0% likelihood.

If the data are “heads, tails, heads, tails, heads, tails”, then again, your first fair-coin hypothesis seems plausible. If on the other hand you have heads alternating with tails not three pairs but 50 pairs in a row, then you reject that model. It begins to sound like the coin is not being flipped in the air, but rather is being flipped with a spatula. Your new probability model is that if the previous result was tails or heads, then the next result is heads or tails, respectively, with 100% likelihood.

 

 

 

 

 

 

 

 

 

 

 

 

Source: https://johnkerl.org/doc/prbstat/prbstat.html

How to bruteforce science or even a theory of everything

Step 1: make a database of all physics papers

Step 2: use a certain program to find probability of certain words coming up and which words follow after that word (using for example Markov Chains)

Step 3: let the program churn out papers and read them, see if there randomly pops out a paper that is brilliant and unlocks the key to physics.

 

Example of an entropic force

 

Analogy with springs. at (b) a rubber band molecule

 

There are more configurations of the polymer molecule being crumpled up then it being stretched out. So the ‘entropy’ of a stretched polymor molecule (or high R) is lower than a crumpled up molecule.

If the molecules are randomly moving around, it will seem like there is a restoring force, pulling the stretched out molecule back to the crumpled molecule. This is a purely statistical force, and it is called an entropic force.

Here is another graph

It is the same reason blowing up a balloon costs energy:

A statistical example of this force is the ‘regression to the mean’. This is not a causal relation.

 

A cool video about Regression to the mean.

 

 

Blackbody radiation of a starting line of a marathon in Boston

 

Courtesy to bear1308 on reddit.

 

It almost looks like a blackbody radiation curve. I wonder what the underlying analogies are.

The paradoxical succes of statistical mechanics

So the problem to apply classical mechanics to every particle in a gas is that there is just too many particles and collisions going on. Any degree of uncertainty would immediately exponentionally grow.

{Uncertianity goes exponentially for each application of classical law}

{Uncertainty decreases exponentially for a statistical law}

The accuracy of statistics is, however, rises with increasing numbers. So even though increasing numbers decreases the accuracy of applying mechanics, it increases the statistics. The fact that there are billions and billions collisions and particles going on in a gas is advantegous for applying statistics! This is because it evens out the uncertainty or bias.

You dramatically decrease the precision of classical mechanics, but you dramatically increase the precision of statistical mechanics!

Statistics: Random Variables

Random variables

Random variables are at the core of statistics. I had a hard time truly understanding what these are, since they are not at all like normal variables e.g. in ‘y=ax’.

I now see them as ‘dices’. A random variable X does not have a value, but has

1. Multiple possible values &
2. A probability distribution

In that sense I think the name Random Variable feels wrong. Some books say that Random Variables are actually ‘functions’. They ‘assign’ numbers to ‘events. Maybe, but even as a function it still feels wrong. Functions have something deterministic about them and random variables not. A better name would be the Random Set X.

Visualisation what a Random Variable does (X is Random Variable)

For example, the ‘Random Variable’ of a coin is:

Its distribution would be:

Surprising probability distribution of a coin toss.

So as I said, random variables are at the core of statistics. We measure them, we want to know their probability distributions and their values in different circumstances.

Another example is dice. It has:

1. As possible values: 1,2,3,4,5,6
2. As a probability distribution:

One dice has as probability distribution that is somewhat constant. If you add dices you see that something interesting happens: it converges toward a ‘gaussian’ curve. This is called the ‘Central Limit Theorem’ and is very important for statistics. I will make another post about this interesting statistical concept. If you play ‘Settlers of Catan’ you will probably recognize the second probability distribution. Satan himself created ‘The Robber’-rule when you throw 7.

A common place where humans like to play with Random Variables.

The four essential Random Variables in common statistics are:

1. The Z-variable with the standard normal distribution.
2. The t-variable with its t-distributions.
3. The χ²-variable (Chi-square), with it’s χ²-distributions.
4. The F-variable with its F-distributions.

I will make posts about each of them in detail. Here I quickly gloss over the details:

The t-, χ²– and F are all derived from the Z-variable.

The χ²-Random Variable is a sum of squared Z-variables

The F-variable is a ratio of χ²-variables.

The t-variables is a special case of the F-variable.

Schrödingers cat is a Random Variable!

What’s the point?

So what is the point of these theoretical variables? Measuring in science is inherently random. Examples are, percentage females in a bus, the length of the next customer, the amount of money in someones wallet. In modeling this, we use appropriate versions of the above four Random Variables and more. They are utilized in so called ‘parametric testing’, which makes assumptions about the distribution of the variable.

Example

Measuring the length of a person is a random variable. It has certain values (between 10 cm to 230 cm) and it has a distribution. The distribution is approximately normal and so this random variable can be modeled with the z-variable, which also has the normal distribution.

 

Statistics: How to test if your data follows the ‘Normal Distribution’.

To do parametric tests, you need to test your data for normality. Parametric testing needs a smaller sample size for drawing conclusions than non-parametric testing. I use three main tests to check for normality: ‘Eyeballing’, statistical tests and looking at the skewness and kurtosis values.

How to test for normality:

• The ‘Eyeball’-test. Make a histogram of the frequencies, add a Normal Curve with the found mean and S.D. of the data. Then check how good it overlaps the data. This is appropriate for n>50. Q-Q-plots can also help you.

Eye-ball method

• Tests of Normality. There are two tests, each appropriate for certain sample sizes. Shapiro-Wilk< n=50 < Kolmogorov-Smirnov < 300. If the test is significant, the data is not-normal. These tests are notoriously easy to become significant.

Tests of Normality-table in SPSS

• Using ‘skewness’ and ‘kurtosis’.

For n < 50, if the z values of the skewness and kurtosis are greater than 1,96, reject the hypothesis that the data is normal.

For 50 < n < 300, if the z values are greater than 3,29, reject the hypothesis that the data is normal.

For n > 300, look at the absolute skew and kurtosis levels. If the skew value is larger than 2 or kurtosis is larger than 7, reject the null hypothesis.

Reference: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3591587/

Skewness and kurtosis

How to test in SPSS?

1. Histogram + Normal curve: Analyze/Descriptive Statistics/Frequencies.
2. Normality tests: Analyze/Descriptive Statistics/Explore (check ‘Normality plots with test’-box at the ‘Plots’-menu.
3. Skewness and kurtosis: Analyze/Descriptive Statistics/Frequencies