Month: January 2017

Who actually moves slower through time? 

zimbles1 Comment

One of the hardest thing for me to comprohend of special relativity was the fact that an object moving fast through space moves slow through time, but that object sees us also as moving slower through time… this doesnt make sense!

But just as two rockets moving away from each other in outer space, where the question cannot be answered who actually is moving. The question who is actually going slower through time, is also meaningless. It is the exact same question. 

Imagine just two straight lines crossing each other in a plane, which line is actually moving away from the other? This question doesnt make sense, and is exactly the same question as above.. The angle between the lines is what can be measured.

The weird thing about hawking radiation

zimblesLeave a comment

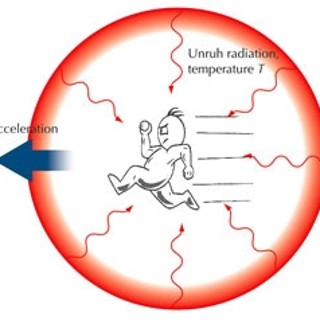
So there are two weird things about hawking radiation

  • It is a thing that actually comes out of black holes. In other words, black holes shine
  • A geodetic observer falling into a black hole will not observe these particles in contrast with the rest of the universe.

In other words, this radiation is relative.

Deriving the Unruh effect in a simple manner.

zimblesLeave a comment

unruh

 

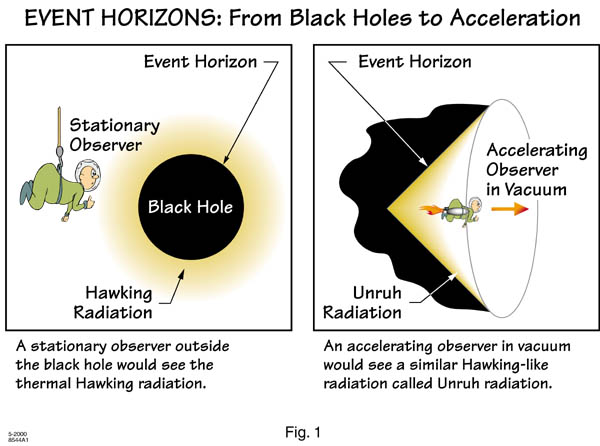
This derivation is based on this paper.

Equations used:

Special relativity:

dt = d\tau \gamma

\frac{dv}{dt} = a (1-\frac{v^2}{c^2})^{3/2}

Integrating over dt we get:

v(\tau) = c \tanh (a \tau / c ) (1)

Equation(s) derived:

T = \frac {\hbar a}{2\pi k c}

Derivation:

First find the hyperbolic orbit of the accelerated (Rindler) observer in the z direction, which are:

t(\tau) = \frac{c}{a} \sinh (\frac{a\tau}{c})

z(\tau) = \frac{c^2}{a} \cosh(\frac{a\tau}{c})

Then consider a plane wave with angular frequency omega_k and wave vector K parallel to the direction z. The lorentz transformation of the angular frequency omega_k looks like:

\omega_k'(\tau) = \frac{\omega_k - Kv(\tau)}{\sqrt{ 1-v^2(\tau)/c^2)}}

If we substitute equation (4) in the last equation we get:

\omega_k'(\tau) = \frac{\omega_k - K c\tanh (a\tau /c) }{\sqrt{ 1-\tanh^2 (a\tau /c) )}}

With K = \omega_k/c we get:

\omega_k'(\tau) = \frac{\omega_k (1 - \tanh (a\tau /c) ) }{\sqrt{ 1-\tanh^2 (a\tau /c) )}}

Then do some complicated algebra shown with \tanh (a\tau/c) = b

First step: \frac{1-b}{\sqrt{1-b^2}} = \frac{\sqrt{ (1-b)(1-b) }}{\sqrt{(1-b)(1+b)}} = \frac{\sqrt{ (1-b) }}{\sqrt{(1+b)}}

Use this hyperbolic identity

Second step

Conclusion:

\omega_k'(\tau) = \frac{\omega_k (1 - \tanh (a\tau /c) ) }{\sqrt{ 1-\tanh^2 (a\tau /c) )}} = \omega_k e^{-a\tau/c} (2)

Now consider the time-dependent phase, which is determined by:

\phi (\tau) = \int_{\tau} \omega'_k(\tau') d\tau'

Plugging in equation (2) and integrating we get for the phase:

\phi (\tau) =\frac{c}{a} \omega_k e^{-a\tau/c}

Where the frequency spectrum S is determined like:

S(\Omega) = |\int_{\infty}^{\infty} d\tau e^{i \Omega \tau } e^{i \phi }|^2

Substituting our formula we get a hard looking integral:

S(\Omega) = |\int_{\infty}^{\infty} d\tau e^{i \Omega \tau } e^{i (\omega_k c/a) e^{a \tau/c} }|^2

This integral looks hard and I can’t solve it, if we look at page 4 of the paper we can see it equals an equation that looks like a Planck Law.

S(\Omega) = \frac{2 \pi c}{\Omega a}\frac{1}{e^{2\pi \Omega c/a} - 1}

Which looks like the planck law

E= \hbar \Omega \frac {1}{e^{\hbar \Omega / kT} -1}

If we compare the following factors:

(e^{2\pi \Omega c/a}-1)^{-1}

(e^{\hbar \Omega / kT} -1)^{-1}

Now we equate them for reasons I don’t get:

(e^{\hbar \Omega/ kT} -1)^{-1} =  (e^{2\pi \Omega c/a}-1)^{-1}

And we get:

\frac {\hbar \Omega}{kT} =  2 \pi \Omega \frac{c}{a}

Rearranging:

\hbar / kT =  2 \pi c/a

Solving for T, temperature:

T =  \frac {\hbar a}{2 \pi kc}

We get the unruh temperature.

figure1